Binary Search Trees



First off, we've got the Node class. This is the basic building block of our tree. It has three properties: value, left, and right. value holds the node's data, while left and right point to the node's left and right children, respectively. These start off as null, as empty as my coffee cup at the end of the day!
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}Now, we fly into the BinarySearchTree class. On creation, it has just one property - root. This is the starting point of our tree, which initially is null, symbolizing our tree is empty. It's like an empty canvas waiting to be painted!
class BinarySearchTree {
constructor(){
this.root = null;
}
}Moving on to the insert method. It accepts a value, creates a new node, and places it at the correct spot in the tree.
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}Next, the find method. It's on the hunt for a specific value.
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}Now comes the contains method. It's very similar to find, but instead of returning the node, it returns a Boolean.
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}Next up, the bfs method. 'Bfs' stands for Breadth-First Search. (we should use queue data structure here, but on an interview you would just explain to the interview you will pretend this array is a queue for time sake but if you were implementing it in production you would use a queue for its superior time complexity on adding things to the front and dequeue ing them)
bfs(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}Finally, we come to the trio of dfsPreOrder, dfsPostOrder, and dfsInOrder methods. These are all about Depth-First Search. They dive deep into the tree before coming up for air!
dfsPreOrder visits the root first, then the left child, and finally the right child. dfsPostOrder starts with the left child, then the right, and ends at the root. dfsInOrder goes left child, then root, and finally right child. In each method, the visited node's value is added to an array, showing different views of the tree.
dfsPreOrder(){
let data = [];
function traverse(node){
data.push(node.value);
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
dfsPostOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value);
}
traverse(this.root);
return data;
}
dfsInOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
data.push(node.value);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}Binary Search Tree properly implemented
Binary Search Tree (BST)
BST
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);Breadth First Search
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
bfs(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);
tree.bfs();Depth First Search
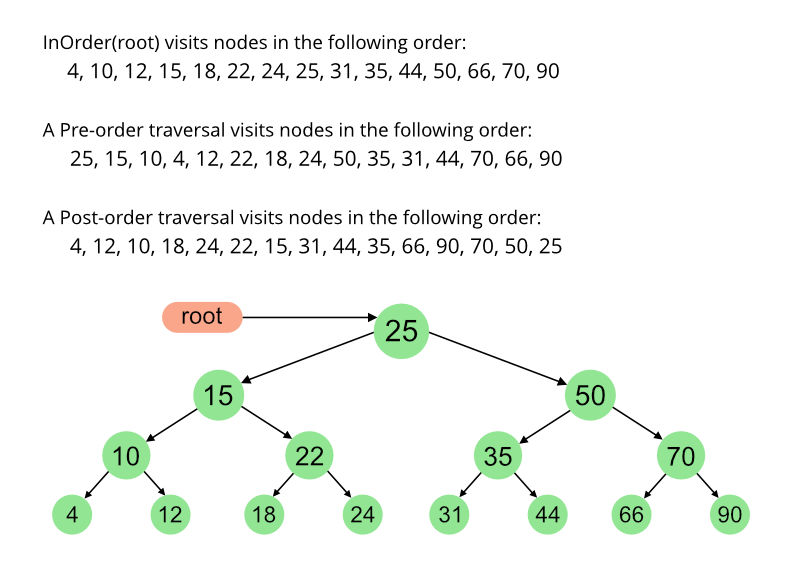
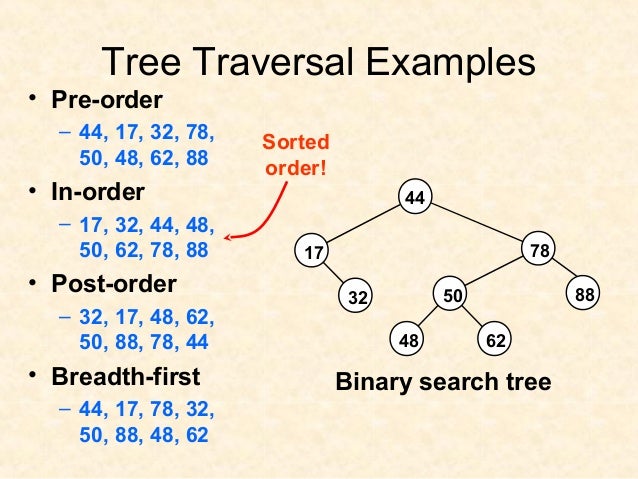
Algorithm Inorder(tree)
Traverse the left subtree, i.e., call Inorder(left->subtree) Visit the root. Traverse the right subtree, i.e., call Inorder(right->subtree)
Algorithm Preorder(tree)
Visit the root. Traverse the left subtree, i.e., call Preorder(left->subtree) Traverse the right subtree, i.e., call Preorder(right->subtree)
Algorithm Postorder(tree)
Traverse the left subtree, i.e., call Postorder(left->subtree) Traverse the right subtree, i.e., call Postorder(right->subtree) Visit the root
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
bfs(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}
dfsPreOrder(){
let data = [];
function traverse(node){
data.push(node.value);
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
dfsPostOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value);
}
traverse(this.root);
return data;
}
dfsInOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
data.push(node.value);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);
tree.dfsPreOrder();
tree.dfsPostOrder();
tree.dfsInOrder();